728x90
그래프(Graph)는 객체 간의 연결 관계를 표현하는 자료구조
노드(Node) 또는 정점(Vertex)과 이를 연결하는 간선(Edge)으로 구성됨.
그래프의 활용
그래프는 연결 관계를 표현하는 자료구조로, 현실 세계의 다양한 개체와 관계를 모델링할 수 있음
- SNS 분석
- 사용자 간의 팔로우 관계
- 교통망 & 지도 데이터
- 도시, 도로
- 정거장, 정거장 연결 선
- 컴퓨터 네트워크
- 라우터와 그 연결 관계
종류
무방향 그래프 (Undirected Graph)

간선에 방향성이 없는 그래프, 두 노드는 `양방향`으로 연결됨
A → B로 갈 수 있고, B → A로 갈 수 있음 = 서로 연결된 상태
방향 그래프 (Directed Graph)

- 간선에 방향성이 있는 그래프, A → B로 향하면, A에서 B로만 이동 가능
- 들어오는 간선과 나가는 간선으로 구분 가능
- 들어오는 간선 = `indegree`
- 나가는 간선 = `outdegree`
비가중치 그래프(Unweighted Graph)

모든 간선이 동일한 가중치 (또는 가중치X)를 가진 그래프
가중치 그래프 (Weighted Graph)

- 간선마다 가중치가 할당된 그래프
- 가중치는 거리, 비용 등 다양한 값을 나타낼 수 있음
📌 다익스트라, 플로이드 워셜 알고리즘에 사용됨!
순환 그래프 & 비순환 그래프
- 순환 그래프 (Cyclic Graph)
- 적어도 하나 이상의 `사이클`이 존재하는 그래프
- 비순환 그래프 (Acyclic Graph)
- 사이클이 존재하지 않는 그래프
- 트리, 방향 비순환 그래프 (DAG)
DAG는 방향성이 있는 비순환 그래프 中 사이클이 없는 그래프
`위상정렬`이 가능하다.
그래프 표현
컴퓨터에게 그래프를 표현하려면 어떻게 해야할까?
👉 적절한 자료구조를 이용해서 표현해야 함.
인접 행렬 (Adjacency Matrix)
`2차원 배열`을 이용하여 노드 간의 연결 관계 저장
연결되어 있으면 `1`, 그렇지 않으면 `0` 기록
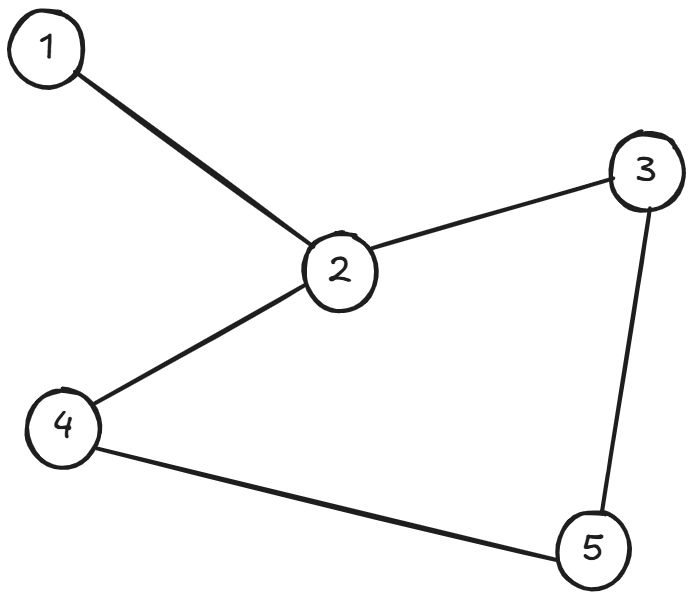
이 그래프에서 정점을 행과 열로 정렬하여 관계를 나타낼 수 있음

int[][] matrix = {
{0,1,0,0,0}, // 1
{1,0,1,1,0}, // 2
{0,1,0,0,1}, // 3
{0,1,0,0,1}, // 4
{0,0,1,1,0}, // 5
};위 그래프의 특징은 자기 자신을 연결하는 간선 (`A-A`)이 없으므로 대각선의 모든 값이 `0`임
무향 그래프이므로 대각선을 기준으로 대칭을 이룸
📌 희소그래프인 경우 비효율적임!
희소그래프 = 정점 수는 많지만, 간선의 개수가 적은 경우
인접 리스트 (Adjacency List)
각 정점에 연결된 다른 정점들을 리스트 형태로 저장하는 방식
연결된 정점만 저장하므로, 불필요한 메모리 낭비를 줄일 수 있어 희소 그래프에서 매우 효율적
두 가지 형태로 구현 가능
- `리스트` 활용: 정점 번호가 0부터 시작하는 경우
- `Map` 활용: 정점 번호가 숫자가 아니거나 0부터 시작하지 않는 경우

리스트 구현
List<List<Integer>> graph = List.of(
List.of(2), // 1
List.of(1, 3, 4), // 2
List.of(2, 5), // 3
List.of(2, 5), // 4
List.of(3, 4), // 5
);맵 구현
Map<String, List<String>> graph = new HashMap<>() {{
put("1", List.of("2")); // 1
put("2", List.of("1", "3", "4")); // 2
put("3", List.of("2", "5")); // 3
put("4", List.of("2", "5")); // 4
put("5", List.of("3", "4")); // 5
}};
728x90
