728x90
그래프에서는 모든 정점을 방문해야 할 때가 자주 있다.
모든 정점을 방문하는 방법은 다양하지만, 대표적으로 BFS와 DFS 방법을 사용할 수 있다.
두 방법은 매우 간단하나, 그래프 알고리즘에서 핵심적인 위치를 차지한다.
∴ 두 탐색 방법에 대해 아주 깊은 직관을 가져야 할 필요가 있다.
트리에 대해 BFS, DFS 수행

- 루트를 시작으로 탐색을 한다면 `BFS`는 먼저 루트의 자식을 차례로 방문함,
- 다음으로 루트의 자식의 자식, 즉 루트에서 두 개의 간선을 거쳐서 도달할 수 있는 정점을 방문
= 루트에서 가까운 거리 순으로 방문
- `DFS`는 루트의 자식 정점을 하나 방문한 다음 아래로 내려갈 수 있는 곳까지 내려감
- 더 이상 내려갈 수가 없으면 위로 되돌아 오다가 내려갈 곳이 있으면 즉각 내려감
일반적인 그래프 G =(V, E)에 BFS, DFS 수행
1) BFS 수행

- 시작 정점으로 정해진 정점 방문 (1)
- 1에서 방문한 정점에 인접한 정점 모두 방문 (2, 3, 4)
- 정점 2에 인접한 정점 중 방문하지 않은 정점은 없음
- 정점 3에 인접한 정점 중 방문하지 않은 정점 모두 방문 (5)
- 정점 4에 인접한 정점 중 방문하지 않은 정점 모두 방문 (6, 7)
- 정점 5에 인접한 정점 중 방문하지 않은 정점은 없음
- 정점 6에 인접한 정점 중 방문하지 않은 정점 모두 방문 (8)
- 정점 7에 인접한 정점 중 방문하지 않은 정점은 없음
- 정점 8에 인접한 정점 중 방문하지 않은 정점은 없음
📌 너비 우선 트리
그림에서 검은색 굵은 간선은 각 정점을 처음으로 방문할 때 사용한 간선임
그래프에서 이 간선들만 남기면 트리가 되는데, 이를 너비 우선 트리라고 함
BFS 알고리즘 기술
BFS(start) {
Set<Integer> visited = new HashSet<>();
Queue<Integer> queue = new LinkedList<>();
visited.add(start);
queue.add(start);
while (!queue.isEmpty()) {
int node = queue.poll();
for (int neighbor : graph.getOrDefault(node, new ArrayList<>())) {
if (!visited.contains(neighbor)) {
visited.add(neighbor);
queue.add(neighbor);
}
}
}
}- 시작 정점을 제외한 모든 정점을 방문하지 않은 상태에서 시작.
- 큐의 맨 앞에 있는 정점(시작점)을 빼내고 이에 인접한 정점 중 방문하지 않은 정점을 모두 방문표시 후 큐에 삽입
- BFS에 수행되는 동안 add()와 poll()을 정확히 V번 호출 = 각 정점이 큐에 한 번씩 들어갔다가 나옴
- `시간 복잡도: O(V + E)`
❓ 왜 O(V+E)인가?
정점은 한 번만 큐에 들어가고 한 번만 방문 처리되므로 O(V)
각 간선은 양 끝점 중 하나에서만 확인되므로 O(E)
무방향 그래프의 경우, 각 간선은 두 정점에서 한 번씩 확인되지만,
중복 체크를 통해 한 번만 큐에 들어가므로 결국 총 E개의 간선만큼 순회함
2) DFS 수행
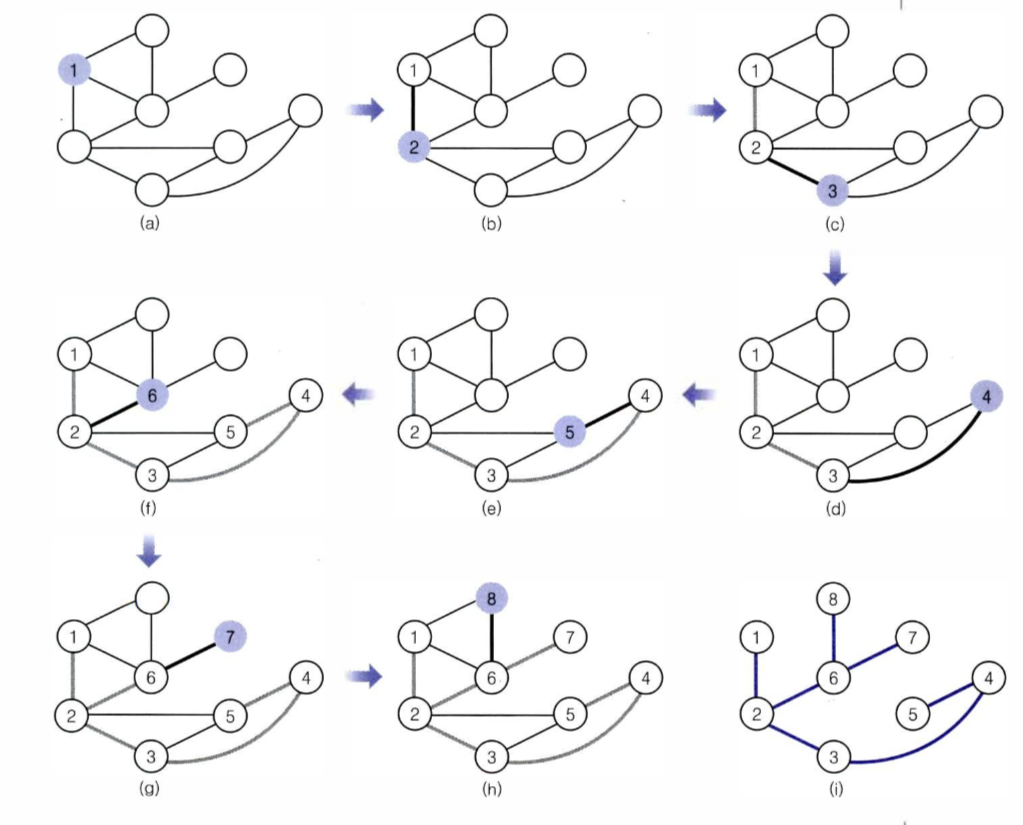
- 시작 정점으로 정해진 정점 방문 (1)
- 정점 1에 인접한 정점 중 하나 방문 (2)
- 정점 2에 인접하면서 방문하지 않은 정점 방문 → 3개 中 하나 방문 (3)
- 정점 3에 인접하면서 방문하지 않은 정점 방문 → 2개 中 하나 방문 (4)
- 정점 4에 인접하면서 방문하지 않은 정점 방문 (5)
- 정점 5에 인접한 정점 중 방문하지 않은 정점은 없으므로 왔던 길을 되돌아 감.
- 정점 4, 3에 인접한 정점 중 방문하지 않은 정점은 없음
- 정점 2로 되돌아오면 인접한 정점 중 방문하지 않은 정점 방문 (6)
- 정점 6에 인접하면서 방문하지 않은 정점 방문 → 2개 中 하나 방문 (7)
- 정점 7에 인접하면서 방문하지 않은 정점은 없으므로 왔덜 길을 되돌아 감
- 정점 6으로 되돌아감 = 방문하지 않은 정점X
- 정점 2로 되돌아감 = 방문하지 않은 정점X
- 정점 1로 되돌아감 = 방문하지 않은 정점X
- 시작 정점에서 더 이상 갈 곳이 없으므로 탐색 종료
📌 깊이 우선 트리
검은색 굵은 간선은 각 정점을 처음으로 방문할 때 사용한 간선임
그래프에서 이 간선들만 남기면 트리가 되는데, 이를 깊이 우선 트리라고 함
DFS 알고리즘 기술
DFS(node, visited) {
visited.add(node);
for (int neighbor : graph.getOrDefault(node, new ArrayList<>())) {
if (!visited.contains(neighbor)) {
DFS(neighbor, visited);
}
}
}- 정점 node를 방문하였다고 표시하고, 이와 인접한 정점 중 방문하지 않은 정점에 대해 각 DFS 호출
- 정점 V에 인접한 정점 중 방문하지 않은 정점 x, y, z가 있더라고 x에 대해 DFS를 호출하면 깊이 들어감
- y나 z가 다른 정점과 인접하면 방문될 수 있음
궁극적으로 모든 정점에 대해 DFS가 한 번씩 호출되므로 시간복잡도는 `O(V + E)`
이진 탐색 (Binary Search)
이진 탐색(Binary Search)은 정렬된 배열에서 특정한 값을 효율적으로 찾는 탐색 알고리즘이다.
이 알고리즘의 기본 원리는 탐색 범위를 반으로 줄여가며 데이터를 찾는 것이며,
이 과정을 반복함으로써 탐색의 효율성을 극대화한다.
이진 탐색은 분할 정복(Divide and Conquer) 방식의 대표적인 예시로 볼 수 있다.
기본 원리
- 정렬된 배열: 이진 탐색을 수행하기 전에 데이터가 정렬되어 있어야 한다.
데이터가 정렬되어 있지 않은 경우, 이진 탐색은 올바른 결과를 보장할 수 없음 - 중간점 선택: 탐색 범위 내에서 중간 위치의 요소를 선택,
배열이 0부터 시작한다고 가정할 때, 중간점의 인덱스는 (left + right) / 2로 계산 - 탐색 조건 비교: 중간점의 데이터와 찾고자 하는 값(target)을 비교.이 때, 세 가지 경우가 발생할 수 있음
- 중간점의 데이터 = 찾고자 하는 값: 탐색 종료
- 중간점의 데이터 < 찾고자 하는 값: 탐색 범위의 왼쪽 부분을 버리고 오른쪽 부분을 새로운 탐색 범위로 설정
- 중간점의 데이터 > 찾고자 하는 값: 탐색 범위의 오른쪽 부분을 버리고 왼쪽 부분을 새로운 탐색 범위로 설정
- 새로운 탐색 범위를 기반으로 2번과 3번의 과정을 찾고자 하는 값이 발견되거나 탐색 범위가 더 이상 존재하지 않을 때까지 반복
이진 탐색의 장단점
장점
- 효율성: 이진 탐색은 `O(log n)`의 시간복잡도를 가지므로 대규모 데이터셋에서도 매우 빠름
- 간결함: 알고리즘의 구현이 간결하며, 이해하기 쉬움
단점
- 정렬된 데이터: 데이터가 미리 정렬되어 있어야 함
- 동적 데이터셋: 데이터셋이 자주 변경되어 재정렬이 필요한 경우, 효율 저하
알고리즘 구현
이진 탐색을 구현하는 방법은 크게 재귀적 방법과 반복적 방법으로 나눌 수 있음
재귀적 방법은 함수가 자기 자신을 호출하여 문제를 해결하는 방식이며,
반복적 방법은 while 루프 등을 사용하여 같은 작업을 반복하는 방식입니다.
재귀적 방법
binarySearchRecursive(int[] arr, int target, int left, int right) {
if (left > right) {
return false;
}
int mid = (left + right) / 2;
if (arr[mid] == target) {
return true;
} else if (arr[mid] < target) {
return binarySearchRecursive(arr, target, mid + 1, right);
} else {
return binarySearchRecursive(arr, target, left, mid - 1);
}
}반복적 방법
binarySearchIterative(int[] arr, int target) {
int left = 0;
int right = arr.length - 1;
while (left <= right) {
int mid = (left + right) / 2;
if (arr[mid] == target) {
return true;
} else if (arr[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return false;
}참고
728x90
